Medical Image Segmentation metrics

a semi-technical smorgasbord of the metric spiesekarte

This is a WIP (Work-In-Progress): this message will be removed once sufficient progress has been made.

The 2015 review by Taha and Hanbury [1] segments (pun unintended) image segmentation metrics into six categories:

  1. Overlap: this is based on the four quadrants of True/False Positive/Negative, and are by far the most popular metrics used (especially Dice). Essentially, they measure some ratio of overlap versus the overall set. Unfortunately, in practice - these metrics could be very biased. Specifically, for objects that are larger, the scores are typically not very sensitive to errors, while for smaller objects, the scores become much more sensitive.
Comparison of three popular overlap based metrics - Dice, Jaccard or IoU and F1 score.

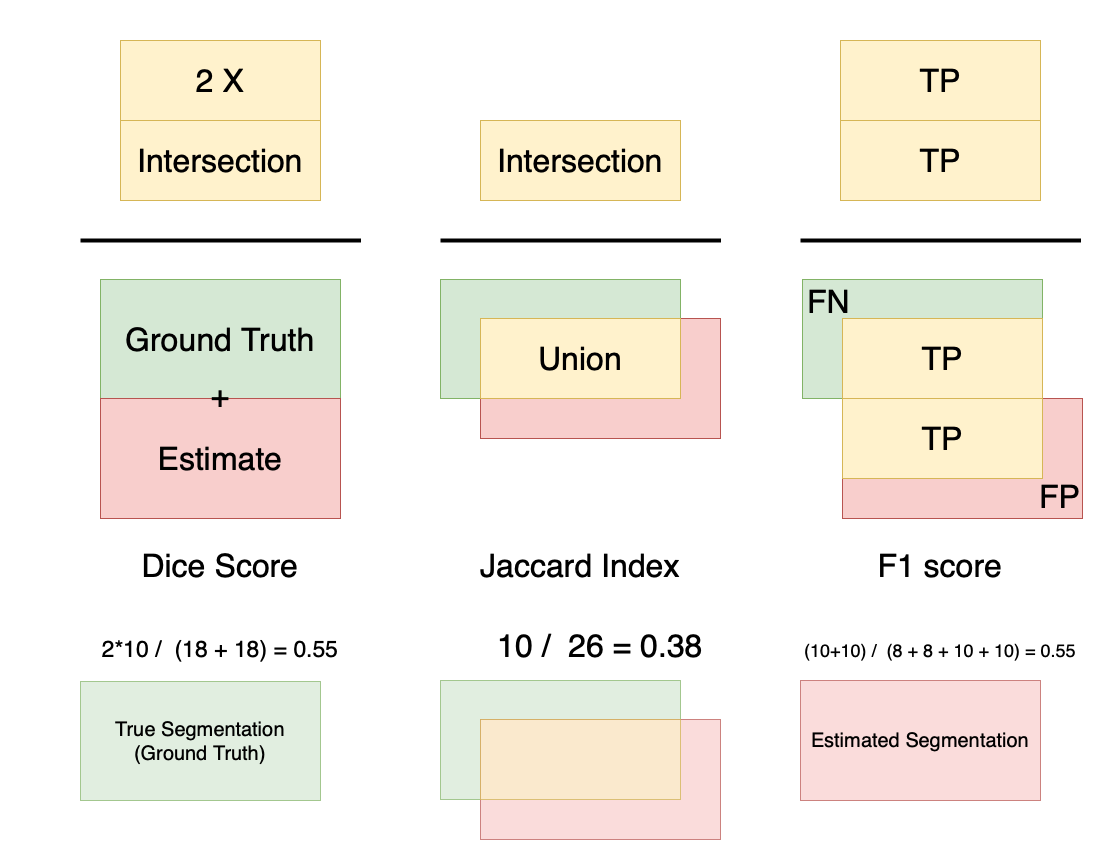
Well known varieties: Dice, Jaccard, F1

  1. Volume: this too depends on the True/False Positive/Negative quadrants, however, it does not consider the intersection at all. It is defined as: 1 - ( False Negative - False Positive )/(Sum of GT and Estimate). Interestingly, this metric can be 1 even when the overlap is empty!

  2. Pair counting: This family involves looking at each segmentation as a set, and then defining the score based on the belonging-ness of each element (imagine as a pixel) in each of the two sets (ground truth or estimate, or both). In the context of image segmentation, this could be reframed as (TP + TN) / (TP + TN + FP + FN), and hence in some way, becomes an overlap metric.

  3. Information theoretic:

Mutual Information

  1. Probabilistic:

AUC, Cohen’s Kappa

  1. Spatial distance:

These include the rather well known Hausdorff, Average, and Mahalanobis distances.

A drawback (which is likely a consequence of how close these metrics are to actual image properties) is that they are not normalized. This makes interpretation and comparison more challenging than otherwise. It could be argued that a ‘true’ numerical measure helps in interpretation, but it then involves more complications like what the pixel dimensions are, are there discretization effects, and so on.

What are the characteristics of an ideal metric?

This is a difficult question to have a generic answer, but here are some high-level expectations:

  1. It is invariant to resolution/size changes (something DSC for example is not)
  2. This is not strictly necessary, but a normalized metric is better than one with an undefined range. This is especially important for comparisons across images.
  3. It is consistent from an outcome perspective. Specifically, for a normalized measure, 0.9 should have a well understood meaning outside the image-space, and should provide some guarantees in the outcome.

Alternative views

Further reads

https://www.kaggle.com/yassinealouini/all-the-segmentation-metrics is a good implementation focused treatment.

https://towardsdatascience.com/metrics-to-evaluate-your-semantic-segmentation-model-6bcb99639aa2 is another good starting point to explore this space.

References

[1] Taha, A.A., Hanbury, A. Metrics for evaluating 3D medical image segmentation: analysis, selection, and tool. BMC Med Imaging 15, 29 (2015). https://doi.org/10.1186/s12880-015-0068-x